Reviving a Suppressed Technology – Part 1
The physics of Dennis Lee’s heat pump
In my recent interview, I was asked about suppressed technologies that could be brought to the public through some kind of political alliance (Green-Party types, in this instance). I replied with the best example that I knew of: Dennis Lee’s heat pump. It is still the world’s best heating system. There is a company in Portugal that makes them, but it is the only company in the world that know of. That heat pump has been completely wiped out in North America. I heard that my public writings have sent some business their way.
I decided to make a series of posts on reviving Dennis’s heat pump, which begins with this one. I never really got to be part of building and selling them, alas. My goal when I became Dennis’s partner was to build, sell, and install those heat pumps and fund free-energy R&D with the profits. That could still be done, but a lot has changed in the 40 years since Dennis’s Seattle company was wiped out. What happened in Seattle was the greatest attempt ever made to bring alternative energy technology to the American public. This series of posts will be a wide-ranging discussion, and this post will show why it is still the world’s best heating system, which will get into thermodynamics a little, but nothing that is not taught in the first week of a thermodynamics class. Here goes.
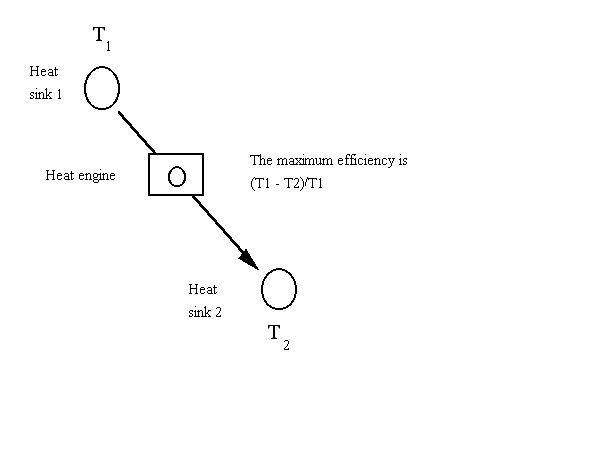
The father of thermodynamics is Sadi Carnot. Carnot’s seminal book was published more than a century after Newcomen built the first commercial steam engine, in an example of how theory could lag practice. For the first time at Substack, I am going to insert some graphics, to make this easier to understand. Carnot theorized that the temperature differential in heat engines would determine their efficiencies. In electric power plants with a 2,000-degree-Fahrenheit boiler temperature and a 55-degree body of water that the turbines exhaust to, using the Carnot equation gets an 80% maximum efficiency. That is the ideal. In practice, such an arrangement gets a 40% thermal efficiency, which means that 40% of the energy in the boiler was translated to power by the turbine. The 60% that was not converted to power warms up the body of water that was exhausted to. Here is a diagram of the Carnot ideal for a heat engine.
It is pretty straightforward. Such an electric power plant gets 50% of the Carnot ideal (40% divided by 80%). For a long time, there has been talk about using ceramic components that won’t melt, achieving boiler temperatures of 4,000 degrees, and coming closer to that Carnot ideal. That has not happened, to my knowledge, and the best gas turbines today get 46% efficiency (and more than 60% when more than one heat engine is used in series).
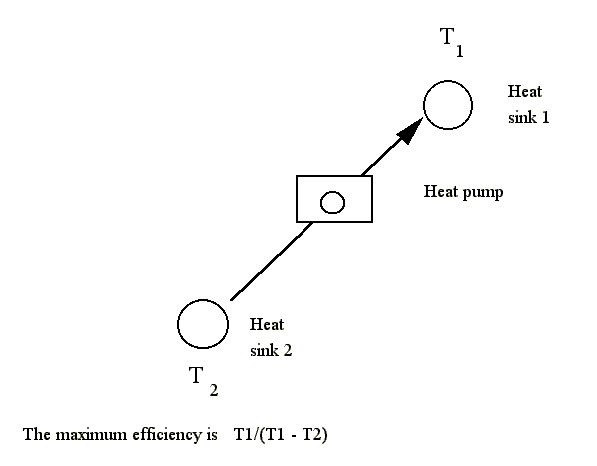
A heat engine moves heat to produce power. A heat pump is the opposite idea, of using power to move heat. The ideal heat-pump efficiency is the reverse of the heat-engine equation, which I present below.
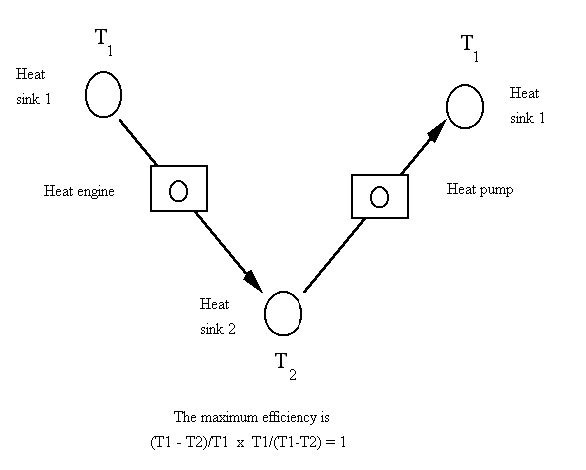
If you combine that heat-engine equation with that heat-pump equation, using the same temperatures for each, the result is one, as seen below.
That means that all of the energy turned into work in the heat engine would power a heat pump that would put all of the energy back in the boiler, to do it again. But real-world systems have friction and heat losses, so that result of one is never attained. If we use 50% of the Carnot ideal for both the heat engine and heat pump, then the result is 0.25, which means that only 25% of the energy in the boiler would make it back to the boiler. There is more on that in coming posts.
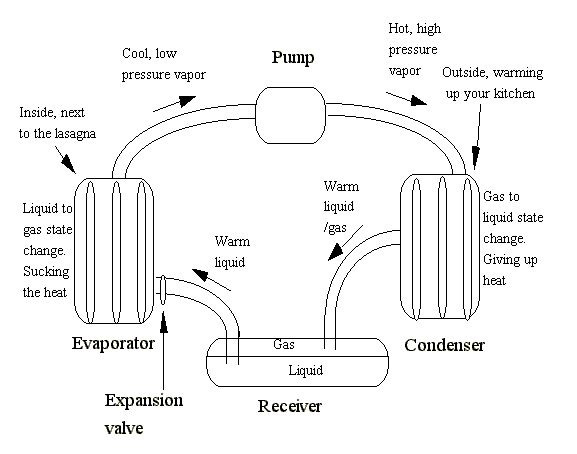
For a heat pump, and I’ll present the ideal case of an air-to-air heat pump, when the outside temperature is 40 degrees Fahrenheit and the house is being heated at 72 degrees, the maximum efficiency is called a coefficient of performance (“COP”) of 16.6. Back in the 1970s, when Dennis’s heat pump was invented, at 40 degrees, the COP was two at maximum, which is 12% (2/16.6) of the Carnot ideal. A refrigerator is a heat pump, and here is a diagram that I made many years ago on how they operate.
I have discussed these issues with scientists and technicians, and efficiencies can be increased by improving the components, such as the heat exchangers. The greater the surface area of contact between the fluids (air, refrigerant, water) that the heat is being transferred between (what a heat exchanger does), the higher the efficiencies. That is really pretty simple.
The surface area of contact with the environment that an air-to-air heat pump has is quite small, on the order of several square feet at best. It is a fin-and-tube array, like can be seen in car radiators. Here is a picture of it:
That fin-and-tube array is called an evaporator, as that is where the refrigerant turns from a liquid to a gas, and absorbs energy as it does. That is why what comes out of aerosol cans is cold. As the liquid turns to a gas, it absorbs heat (called the latent heat of vaporization).
Instead of a tube-and-fin array, Dennis’s heat pump had evaporators that were aluminum panels that the refrigerant ran through. Here is a picture of several evaporator arrays in applications on homes.
Those panels were the exotic component of Dennis’s heat pump. Everything else was standard refrigeration technology that could be bought over-the-counter at industrial parts houses. That panel introduced parameters never seen before in heat pumps. For one thing, instead of the several square feet of evaporator contact with the environment that air-to-airs have, Dennis’s heat pump had eight three-foot-by-eight foot panels, which provided nearly 400 square feet of evaporator contact with the air. That meant that far more heat could be taken from the environment than an air-to-air evaporator could. While an air-to-air heat pump had a few pounds of refrigerant running through it, Dennis’s had 60 pounds. Dennis’s heat pump output about 100,000 BTUs per hour, which was twice what comparable air-to-airs produced, but that was not the most important aspect.
In conditions in which air-to-airs produced a COP of two, Dennis’s heat pump produced a COP of six. Instead of 12% of the Carnot ideal, Dennis’s got 36%, or much closer to the ideal that the best heat engines get. That efficiency was the magic of Dennis’s heat pump.
I have presented the results of several scientific tests of Dennis’s heat pump (1, 2, 3, 4), and there is an interesting story for each of them. In the first one, it led to the inventors’ admitting that they had cut their performance data in half, so that they would not get laughed out of engineering offices over their system’s “impossible” performance. In the second one, one installation at a restaurant in Saint Paul, Minnesota, got a COP of over 5 in January. Air-to-air heat pumps in the Minnesota winter were worthless. In the third one, it was performed by a lab in Arizona for Dennis’s manufacturer for the Seattle company, before the Rockefellers’ bank wiped it out and Dennis had to build his own factory. The fourth one was performed by an engineer who tried to extort us. That test was presented at Dennis’s preliminary hearing, to show how that engineer was unable to think past his textbooks. His mantra was that heat pumps could only output 12,000 BTUs of power per horsepower of the pump (compressor), which was in his refrigeration textbooks. But his data showed 25,000 BTUs, which he considered “impossible,” even after he produced the data himself that proved the “impossible.” He testified to his 12,000 BTU dogma, and then he was presented his own test that showed 25,000 BTUs. That highlights some of the limitations of engineers. I once talked to an installer about why Dennis’s heat pump work so “impossibly,” and he said that Dennis’s system produced twice the pressures of air-to-air heat pumps, which meant higher temperatures, heat output, and efficiencies.
The bottom line was that those panels introduced parameters never seen before in the refrigeration industry, and refrigeration technicians had to discard part of their “education” in order to understand Dennis’s heat pump.
Before writing this post, I looked to see what has changed over the past 40 years in air-to-air heat-pump technology. Some air-to-airs claim COPs of up to nine. But in New Jersey, for instance, when it gets below freezing, air-to-airs can no longer heat a home, so a supplemental heater is needed. That same page mentions some technological improvements, such as variable-speed pumps (AKA compressors) and better refrigerants. If Dennis’s heat pump had not been wiped out, I expect that it would have also benefited from such improvements. I heard of COPs of 12 and 16 with Dennis’s heat pump under ideal conditions, and I am confident that it would still get at least twice the COPs of air-to-airs under the same conditions, because of that panel.
Here is a picture of what happens to air-to-airs when it gets below freezing.
Air-to-air heat pumps blow air through the evaporator to increase the heat exchange, but when ice forms on it, the air cannot get through, which makes the COP plummet, and such heat pumps have electric heaters to defrost the evaporator array, which takes more energy and the COP can dip below one, which means that you are better off with baseboard electric heating than a heat pump, when you need heating the most. In one study, Dennis’s heat pump continued to heat a home and pool in Colorado when the panels were covered under two feet of snow. A team of engineers studied that heat pump and scratched their heads on how it could do it. They hypothesized that the panels simply sucked the heat from the snow, which was replenished by the sunshine and warmer ambient air.
Another aspect of Dennis’s heat pump was that it produced so much heat that it was easier to heat up water than air (water can retain for more heat per unit of volume), so his heat pumps used water instead of air in the heat exchanger (condenser), water tanks of hundreds of gallons were typical with his heat pumps, and swimming pools were often ideal applications. There were costs and benefits of that approach, which I may discuss later.
That is the basic physics, but there are also numerous technical and other issues to discuss, which is coming.